Introduction


Having
understood direction, distance and speed, it is now important to spend some
time in getting to know time, as it impacts aviation. In the previous chapter
we had referred to the formula that we learnt in school i.e. S = ut. In basic
navigation we have no access to distance in the air and thus we have to rely on
flying at a certain speed in a certain direction for a certain time to reach
from A to B. Things would have been simple if the time at all places on the
surface of the earth was same, but it is not so. Can you guess why?
Our body
clock takes its cues from the rising and setting of the sun and thus we have
evolved systems that help us with keeping track of time with respect to the
sun. Since the earth is going around the sun and also revolving around its own
axis, we need to understand the solar system before we can comprehend why we
need different systems like UTC, IST, GMT, LMT, Zone time, etc.
- Why is aviation stuck with
UTC? Is there a better way?
Time and Our Solar System
The ETD of
our flight is 0700Z and the flight duration is 8:00 hours. As we can see in
this statement, we have used time in two distinct ways – as a particular
instant of time and also as a duration of time. Duration of time poses no problem because we have gadgets like watches, clocks that can give us the duration very accurately. However, the basic datum against which we set the clock or watch is what is of greater concern to us since we have many different
standards of time, or datum.
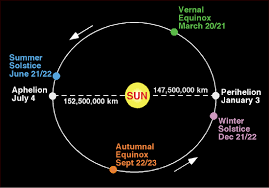
However, taking due cognizance of our body bio-rhythmic clock, the basis of our time-keeping or datum has to be the Sun. We had studied the solar system in an earlier chapter. It must be understood that our solar system comprises the sun and nine major planets, including our earth, revolving around it in elliptical orbits. Each planet is at a different distance from the sun; with Mercury being the closest taking 88 days to complete one orbit; and Pluto being the farthest taking 249 years to complete one orbit around the sun. The motion of all these planets around the sun follows the Kepler’s laws of Planetary Motion, which are as follows: -
However, taking due cognizance of our body bio-rhythmic clock, the basis of our time-keeping or datum has to be the Sun. We had studied the solar system in an earlier chapter. It must be understood that our solar system comprises the sun and nine major planets, including our earth, revolving around it in elliptical orbits. Each planet is at a different distance from the sun; with Mercury being the closest taking 88 days to complete one orbit; and Pluto being the farthest taking 249 years to complete one orbit around the sun. The motion of all these planets around the sun follows the Kepler’s laws of Planetary Motion, which are as follows: -
·
Each planet follows an elliptical orbit around the sun, with the
sun being at one of the foci of the ellipse. When viewed from the North
celestial Pole, the planets orbit in an anti-clockwise direction.
·
The line joining the planet to the Sun sweeps out equal areas in
equal time, or,
o
Distance from sun increases – Speed of orbit reduces
o
Distance from sun reduces – Speed of orbit increases.

(All Images in this post are courtesy of Google Images. Please let me know of any copyright, and I would most willingly remove the images.)
Earth’s Motion
- Rotates
West to East about its axis of rotation
- Makes
one orbit around the sun in about 365 days, 5 hours, 48’ and 45”.
- Axis of
rotation of the earth tilted at an angle of 66.5° to the orbital plane or
putting it another way at an angle of 23.5° from the normal to the orbital plane.
Seasons on the Earth
Seasons on
the earth are caused primarily due to the tilt of the earth’s axis. This causes
the sun to be directly over 23.5° N in midsummer in the Northern hemisphere and
over 23.5° S in mid winter over the Northern hemisphere. When it is summer in
the Northern hemisphere, it is winter in the Southern hemisphere and vice
versa.
- Why is it winter in the
Southern hemisphere when it summer over the Northern hemisphere?
We would now
talk only in terms of the Northern hemisphere. The following takes place:
- Summer: Earth is farthest from the
sun (Aphelion) around 03 July with the Northern hemisphere tilted directly
towards the sun; the sun being over its Northern most point on the earth,
i.e. over the Tropic of Cancer (around 21 June), also known as the summer
solstice for the Northern hemisphere
- Winter: Earth is nearest to the sun
(Perihelion) around 03 January with the Southern hemisphere tilted
directly towards the sun; the sun being over its Southernmost point on the
earth, i.e. over the Tropic of Capricorn (around 22 December), also known
as the winter solstice for the Northern hemisphere.
- Equinox: In between the two
solstices are the spring (around 21 March) and the autumn (around 23
September) equinox (equal night), when the sun is directly over the
equator leading to equal day and night on all parts of the earth.
Understanding Time and Different
Types of Day that Man has devised
Sun’s Apparent Motion: As we have
already discussed, the earth rotates around its own axis from West to East, or
in an anti-clockwise direction when viewed from above the North Pole. If we
consider the earth to be stationary, then it would appear that the sun travels
around the earth in an East to West or clockwise direction. This is the reason
why we say that the sun rises in the East and sets in the West. Also, while so traveling,
the sun would cross all meridians of the earth.
Transit: The
crossing of a meridian by a heavenly body is termed as a transit.
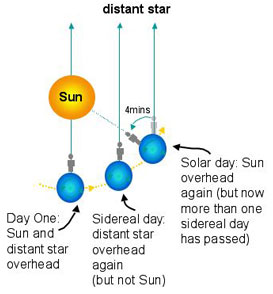
Sidereal Day: Two
successive transits of a star is called a sidereal (star) day. One point that
needs to be understood here is that stars are many light years away from the earth; whereas the earth is only 8 light minutes away from the sun. The
long distance (infinite for all practical purposes) between the stars and the earth ensure that there would be
negligible effect of the earth’s elliptical orbit around the sun on the time
between two transits. This time is very nearly constant and is the time taken
for the earth to complete one full 360° rotation around its own axis. This time
is approx. 23h and 56’, and is called a sidereal day.

Apparent and Mean Solar Day: The motion
around the sun is a little more involved. When viewed from the earth, the sun’s
apparent clockwise motion around the earth would take approx 24 h for two
successive transits if the earth were not revolving around the sun (same as a
sidereal day). However, because the earth is revolving around the sun in approx
365 days (or it is traversing 1°/ day approx), it can be said that the
successive transit would take place only after the earth has rotated through
361°. In addition, the motion of the earth around the sun follows Kepler’s law
and is thus not at a constant speed because the earth’s distance from the sun
is varying. Thus the apparent (True sun) solar day would also vary, and would
not be a constant. This would be very inconvenient for timekeeping purposes. To
overcome this problem, a mean solar day of 24 hours (the average value of the
apparent solar days throughout the year) has been devised.
The Mean Sun: The mean
sun is an imaginary body that moves approx with the apparent (real) sun –
sometimes ahead and sometimes behind it. This mean sun ensures that our days
are always 24 h, and very close to the real days. The discrepancy between the
real (true or apparent sun) and mean sun (devised sun) is about 16’ later in
November and about 14’ early in February. This discrepancy between the real and
the mean sun is called the equation of time.
Leap Year
The earth
takes 365d 5h 48’ and 45” to complete one orbit around the sun, and this is the
astronomical year. Our seasons are as per this astronomical year. However, our
calendar has only 365 d in a year, so if we do not add a day every fourth year,
we would lose approx 6 h off our calendar every year. This would lead to
seasons occurring in different months, over time. To ensure that the calendar
year is synchronized with the seasons or astronomical year, an extra day is
added to the month of February in every fourth year (a year that is divisible
by 4 or leap year). The only exception to this rule is the century, when only
every fourth century is a leap year (1600, 2000, and 2400). This is because in
the leap years, we are catering for 6h instead of the actual 5h 48’ and 45”,
and this time discrepancy has to be adjusted once in every 400 years. All this
is done to keep the stability of seasons so that they occur on around the same
dates every year.
Mean Solar Time and Arc
The mean sun
takes 24 h to go around the earth, or 360° of arc. Its motion in degrees of
longitude and time can thus be worked out as follows: -
- Time Arc
of Longitude
- 24 h = 360°
- 1h = 15° (360°/ 24h)
- 4’ = 1°
- 1’ = 15”
Local Mean Time (LMT)
Local mean
time is the time kept using the observer’s local anti-meridian and the mean sun
in the following manner: -
- Day
starts (0000 h) when mean sun at anti-meridian, and ends after 24 h (2400
h) with sun on the same anti-meridian.
- As the
mean sun goes around the earth in a clockwise direction, any place East of
the observer’s meridian would be ahead of the observer’s LMT, and any
place West of this would have a LMT behind the observer’s LMT. The LMT can
be calculated by using the arcs of longitude, as given above.
Universal Coordinated Time (UTC)
LMT at each
meridian would be different. This would pose certain problems. Thus there was a
need to have a time that was same all across the world. This time was the GMT
or Greenwich Mean Time, or the LMT at Greenwich. The modern name for GMT that
is approved by ICAO is UTC. It is the same as the GMT for all practical
purposes, and is also the standard time used for all aviation related
activities. However, this cannot be used for normal living by all people around
the earth due to our body bio-rhythms.
Zone Times
In this
system, each zone comprises of 15° of longitude (1 hour) and has a zone time.
There are a total of 25 zones, starting with ‘Z’ (from 7.5°W to 7.5°E) and
every 15° thereafter. Time zones around the International Date Line are only
7.5°. The time zones comprise the letters of the alphabet except ‘J’. The numbers in blue are to be added to the UTC to get the zone time; and the numbers in purple are to be substracted from teh UTC to get the zone time.

Standard Time
Zone time
runs in to problems when countries stretch across more than one time zone.
There is thus a need felt to have a standard time for the entire country or for
designated parts of the country. This is the standard time for that country.
IST is the LMT at Allahabad (82.5°E). This is used as a standard time for the
whole of India. Longitude 82.5°E falls on the line between E and F time zones
and thus IST is also referred to as EF. Countries like USA and Canada have more
than 1 standard time. Standard times cannot be calculated unlike zone times.
One needs to refer to tables to find the standard time.
Summer – Daylight Saving Time
As one goes
away from the equator, the days are much longer in summer. To conserve energy,
some countries that are in the higher latitudes have introduced something known
as Daylight Saving Time during summer (which is six months apart in the
Northern and the Southern hemisphere). Actual dates are published in the time
charts. It is easy to remember the changes to the clock by the following rhyme:
-
- Spring
forward in spring
- Fall
back in fall.
International Date Line (IDL)
The
anti-meridian to the Prime Meridian is the general reference for the
International Date Line. It does not follow the meridian exactly, but is curved
at a few places to accommodate populated areas to one side of the date line.
The
significance of the IDL is that the date changes when one crosses the IDL
towards Easterly or Westerly direction, in the following manner: -
- Traveling
on an Easterly heading – subtract one day from the date or lose a day.
- Traveling
on a Westerly direction – add one day to the date or gain a day.
Time however
continues to be the same. To prevent problems when crossing the IDL during a
flight or in calculations, it is advisable to work in UTC before changing over
to ST or LMT.
Thumb Rules
- Longitude
East, UTC least
- Longitude
West, UTC best.
- Easterly
direction travel across IDL – Lose a day
- Westerly
direction travel across IDL – Add a day.
- Arc
times: -
- 24h - 360°
- 1h - 15°


